In the MCD, data are stored in 12 seasonal bins and at 12 local times of day within each season. Although this captures the main seasonal and diurnal components of variability, any intra-seasonal or day-to-day (synoptic) variations are averaged out. Thus there is a need to simulate this variability, especially if the user wishes to produce an ensemble of realizations of a variable at a particular seasonal date and local time of day which covers a realistic range of variability.
In version 1.0 of the MCD large-scale variability in a vertical profile of
a meteorological variable, D(z), was modelled by adding a
series of functions to a mean vertical profile, ![]() ,
,
| |
(6) |
In version 1.0 only correlations in altitude between variables were
considered when calculating the covariance matrix. However, in order to
retain cross-correlations between different variables (zonal wind,
meridional wind, temperature, surface pressure and density) all were
normalized and combined together to form a set of multivariate
functions. Different sets of EOFs were computed for each of the 12 seasons
on a low resolution grid (20![]() longitude
longitude ![]() 20
20![]() latitude) and the series (6) was truncated at N=6 to reduce
the demands on data storage. Even so, typically
latitude) and the series (6) was truncated at N=6 to reduce
the demands on data storage. Even so, typically ![]() of the variance
was retained in the version 1.0 variability model at this level of
truncation.
of the variance
was retained in the version 1.0 variability model at this level of
truncation.
In order to improve the model it is desirable to extend the spatial
dimension to include correlations between variables in both the horizontal
and the vertical. Ultimately it would be desirable to include all the
longitude, latitude and vertical grid-points in the analysis. A technical
point, however, must be noted here. In computing the EOFs, the eigenvalues
and eigenvectors of an ![]() real symmetric matrix must be
found. The order, N, of the matrix depends on the number of variables and
on the number of spatial points. Since the number of calculations needed to
perform the eigenvector problem increases as N3 there is a limit on the
value of N that can be handled practically. The estimated CPU time and
storage requirements for calculating the eigenvectors of the full problem
(even on the low resolution grid with four three-dimensional and one
two-dimensional variables, for which
real symmetric matrix must be
found. The order, N, of the matrix depends on the number of variables and
on the number of spatial points. Since the number of calculations needed to
perform the eigenvector problem increases as N3 there is a limit on the
value of N that can be handled practically. The estimated CPU time and
storage requirements for calculating the eigenvectors of the full problem
(even on the low resolution grid with four three-dimensional and one
two-dimensional variables, for which ![]() ) is prohibitive.
) is prohibitive.
We make the choice, therefore, to calculate EOFs in the two-dimensional, height-longitude plane which gives a manageable set of eigenvector problems. There is some physical basis for this choice, in that much of the variability the model must account for is in the form of baroclinic waves which, in general, propagate West to East along lines of latitude.
In version 1.0 of the MCD we calculated separate sets of the variability
EOFs for each of the 12 seasons. However, due to the relatively small
number of days in each season (50-70), this can lead to poor estimation of
the EOFs. Greater statistical stability can be achieved by forming the
covariance matrix over the entire annual cycle, although this means that
more EOFs must be retained in the series (6) in order to still
capture a relatively high fraction of the variance. Fortunately this is
possible as there is then no need to store the EOFs at each season. In fact
the series can be extended to include 72 (![]() ) EOFs rather than
just 6 per season with no increase in the amount of space needed to store the
MCD.
) EOFs rather than
just 6 per season with no increase in the amount of space needed to store the
MCD.
This also overcomes a problem which might occur with the version 1.0 implementation of the PC modelling. If a time series of a variable was computed across a seasonal boundary there could be a discontinuity at the boundary where the quadratic fit to the intra-seasonal or trend components did not match. In the improved version 2.0 of the variability model we simply store a smooth version of each PC to represent the seasonal cycle together with a variance to represent synoptic activity. This both simplifies and improves the algorithm.
Consider a time series of longitude-pressure vectors of zonal wind,
![]() , meridional wind,
, meridional wind, ![]() , temperature,
, temperature,
![]() , density,
, density, ![]() and surface
pressure
and surface
pressure ![]() at M discrete time points and on L spatial
points. We form a time series of vectors
at M discrete time points and on L spatial
points. We form a time series of vectors ![]() , where
, where
| (7) |
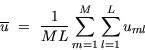 |
(8) |
| (9) |
We then form the ![]() covariance matrix,
covariance matrix, ![]() , such that
, such that
| (10) |
The matrix ![]() is real symmetric and we can find the eigenvectors
and eigenvalues and order them in decreasing eigenvalue magnitude. We
note that if
is real symmetric and we can find the eigenvectors
and eigenvalues and order them in decreasing eigenvalue magnitude. We
note that if ![]() is the ith eigenvector then
is the ith eigenvector then
| (11) |
| (12) |
The ith principal component (PC) at time m, pmi is defined as
| (13) |
| (14) |
Each principal component has 669 values during one year (one per day). From the PCs we calculate a 30 day running mean, psmi, and a variance departure from that mean, pvmi. The modelled PC, p'mi, at time m is then
| |
(15) |
In version 1.0 of the variability model only 6 EOFs per location per season were retained in the series in Equation 6 to limit the amount of data storage required. Because, in the improved version, a single set of EOFs are calculated for the whole year, 72 EOFs can be retained in the series with no greater storage overhead, to give a potentially greater overall variance capture. Figure 5 shows the fraction of variance captured by retaining 72, 36, 18 and 9 EOFs at different latitudes. By retaining 36 EOFs approximately 90% or greater of the variance is captured and by retaining 72 EOFs approximately 95% or greater of the variance is captured. Including more EOFs gives relatively little increase in variance capture but increases the storage requirements considerably. Thus 72 EOFs seems to be a good compromise between variance capture and data storage.
Density is one of the most important variables used by engineers in mission planning (e.g. when calculating entry trajectories or aerobraking manoeuvres). Hence the new variability model is illustrated using this field. Because density varies exponentially with height it is useful to compare any density profile with some `standard' profile. Figure 6 shows the northern hemisphere COSPAR standard atmospheric density profile from the surface to approximately 90 km. All density profiles are referenced to this profile by expressing the density as a percentage difference, d, from the COSPAR profile. i.e.
| (16) |
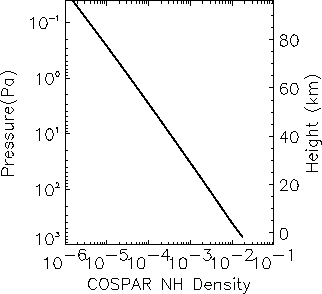 |
Figure 7 shows a selection of instantaneous
longitude-height fields of density (referenced to the COSPAR profiles)
taken directly from the Viking scenario GCM run at ![]() ,
,![]() ,
, ![]() and
and ![]() . The variability model
simulations of these fields are shown in Figure 8. On a
large scale the variability model captures the seasonal cycle of density
variability well. Small differences between the GCM and the variability
model simulated fields are due to the random nature of the PC model
(Equation 15).
. The variability model
simulations of these fields are shown in Figure 8. On a
large scale the variability model captures the seasonal cycle of density
variability well. Small differences between the GCM and the variability
model simulated fields are due to the random nature of the PC model
(Equation 15).
 |