


Next: References
Up: Variability Models
Previous: The Large-Scale Variability Model
The small-scale variability model simulates perturbations of density,
temperature and wind due to the upward propagation of small-scale gravity
waves. The model is based on the parameterization scheme used in the numerical
models that simulated the data in the database (see Collins et. al,
1997).
The surface stress exerted by a vertically-propagating, stationary gravity wave
can be written
| 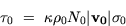 |
(17) |
where 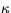 is a characteristic gravity wave horizontal wave number,
is a characteristic gravity wave horizontal wave number,
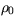 is the surface density, N0 is the surface Brunt
Väisälä frequency,
is the surface density, N0 is the surface Brunt
Väisälä frequency, 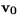 is the surface vector wind and
is the surface vector wind and
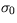 is a measure of the orographic variance. In this case we choose the
model sub-grid scale orographic variance.
The surface stress can be related to the gravity wave vertical isentropic
displacement,
is a measure of the orographic variance. In this case we choose the
model sub-grid scale orographic variance.
The surface stress can be related to the gravity wave vertical isentropic
displacement, 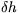 , by
, by
| 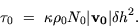 |
(18) |
We then assume that the stress, 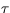 , above the surface is equal to that
at the surface. This leads to an expression for
, above the surface is equal to that
at the surface. This leads to an expression for 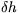 , at height z,
, at height z,
| 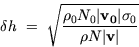 |
(19) |
where 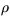 , N and
, N and 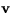 are the density, Brunt Väisälä
frequency and vector wind at height z.
are the density, Brunt Väisälä
frequency and vector wind at height z.
The gravity wave perturbation to a meteorological variable is calculated by
considering vertical displacements of the form
| 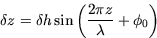 |
(20) |
where 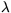 is a characteristic vertical wavelength for the gravity
wave and
is a characteristic vertical wavelength for the gravity
wave and 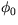 is a randomly generated surface phase angle.
Perturbations to temperature, density and wind at height z are then found
by using the value at
is a randomly generated surface phase angle.
Perturbations to temperature, density and wind at height z are then found
by using the value at 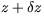 on the background profile, with the
perturbations to temperature and density calculated on the assumption of
adiabatic motion to the valid height. A value can be chosen for
on the background profile, with the
perturbations to temperature and density calculated on the assumption of
adiabatic motion to the valid height. A value can be chosen for 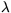 to provide a reasonable comparison with the observed Viking entry
temperature profiles above 50km; we take
to provide a reasonable comparison with the observed Viking entry
temperature profiles above 50km; we take 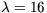 km. An example of
several small scale perturbations is shown in Figure 9.
km. An example of
several small scale perturbations is shown in Figure 9.
Figure 9:
A series of ten perturbations generated by the small scale
variability model added to mean profiles of temperature and density from
the MCD; these correspond to the Viking Lander 1 entry location and time.
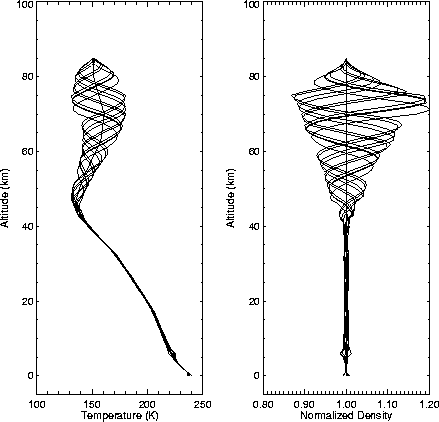 |



Next: References
Up: Variability Models
Previous: The Large-Scale Variability Model
Stephen Lewis
3/10/1999